株式会社Progateでソフトウェアエンジニアをしているsy-tenchoです。本記事は Progate AdventCalendar 2020 19日目 です。
12月と言えばプロ野球選手の契約更改の季節ですね。ということで今日は僕の贔屓球団である読売ジャイアンツの野手の年俸はどのような要因によって決まるのかということをお題に、Pythonを使った統計分析の方法を簡単に紹介したいと思います。
はじめに
僕はProgateでエンジニアをしている傍、大学で経済学などを勉強しています。その中で統計分析をすることがあるのですが、StataやEviewsといった定番ソフトは学校に行かないと使えないし、R言語を一から勉強するモチベーションもあまりないので最近はPythonを使った分析に取り組んでいます。今回は statsmodels というPythonのライブラリを Google Colaboratory 上で動かし、簡単な回帰分析を実際に行ってみようと思います。
テーマ
プロ野球選手の年俸はどのようにして決まるのか?
先日もヤクルトの村上選手が弱冠20歳にして年俸1億円に到達して話題になりましたが、プロ野球選手の巨額な年俸は一体どのような要因によって決まるのかを分析するのが今回のテーマです。
今回は SPAIA や 日本プロ野球機構 のデータを参考に読売ジャイアンツの野手の年俸トップ20の選手の個人成績をまとめ、2019年のクロスセクションデータを作成しました。変数と選出理由は以下の通りです。
- 2020年の年俸
- 本塁打数 (走攻守の攻の要素)
- 四球数 (四球数が多いと出塁率が上がり、チャンスメークに貢献している)
- 盗塁数 (走攻守の走の要素)
- 守備率 (走攻守の守の要素)
- 出場試合数 (たくさん試合に出ている選手は貢献度も高いはず)
- 年数 (ベテラン選手が、成績以外でチームに与える影響は大きい?)
- 外国人選手ダミー (外国人選手は年俸が高いイメージがある)
- 生え抜き選手ダミー (生え抜き選手はより大事にされるのではないか?)
今回は2020年の年俸を被説明変数に、その他の変数を説明変数とした線形モデルを仮定し、重回帰分析を行います。
分析
導入
それでは実際にコードを書いて分析していきます。まずは必要なライブラリをインポートします。
import pandas as pd import statsmodels.api as sm
Google Colaboratoryではローカルからファイルを読み込むかドライブをマウントすることが可能ですが今回は前者を選択します。
from google.colab import files uploaded = files.upload()
データを眺める
インポートしたcsvファイルをpandasのDataFrameの形式で読むことで操作がしやすくなります。
df = pd.read_csv('giants_2019.csv')
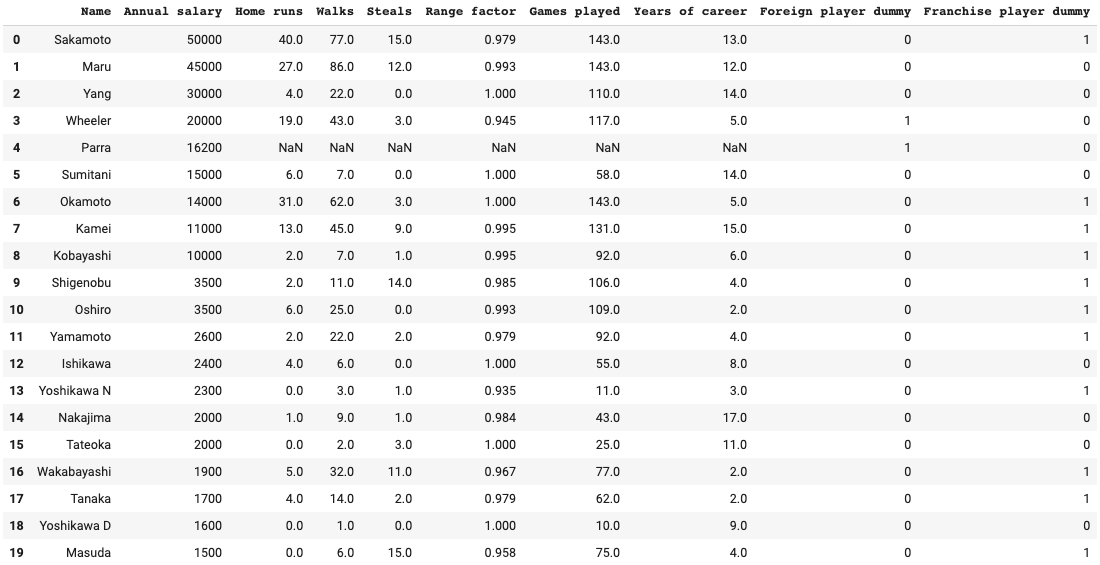
*陽選手は台湾籍ですが、日本国籍の選手と同じ出場資格を持つので外国人ダミーから外しています。
pandasのdescribe()メソッドを呼び、基本統計量を確認します。
df.describe()
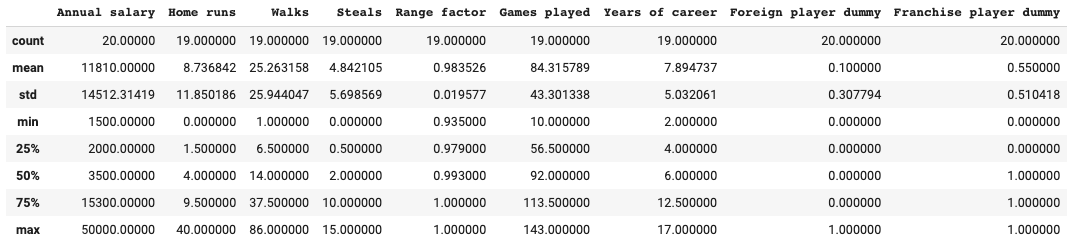
次に実際に回帰分析を回していきたいところですが、パーラ選手は2020年加入で2019までの日本のプロ野球での出場機会がないため、欠損値が発生しています。なのでパーラ選手のデータを省きます。
df.dropna()
*fillna()メソッドを使うことで欠損値を平均値や中央値で補完する方法もよく用いられるかと思います。
df.fillna(df.mean()) df.fillna(df.median())
回帰分析1
ではいよいよ回帰分析を回してみます。今回は線形モデルを仮定していたので statsmodels.regression.linear_model.OLS を使います。年俸を被説明変数(①)、その他を説明変数とします。(②) また、定数項も追加します。③
Y = df[df.columns[1]] # ① X = df[df.columns[2:]] # ② X = sm.add_constant(X) # ③ model = sm.OLS(Y, X) results = model.fit() print(results.summary())
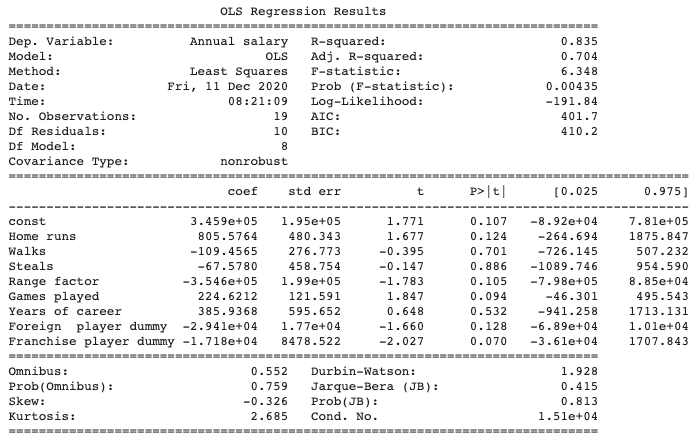
VIF
本来であれば推定量がBLUE(最良線形不偏推定量)となっているか確認するため、様々なテストや検証をする必要があります。今回はその中でも重回帰分析をするときに最もよく使う指標の一つであるVIF(Variance Inflation Factor)を算出してみようと思います。重回帰分析をする時に説明変数同士が相関していると多重共線性という問題を引き起こしますが、VIFを算出することで多重共線性を起こしている可能性のある変数を発見することができます。
statsmodelsは VIFを算出するメソッド を提供しているのでこちらを使っていきます。
from statsmodels.stats.outliers_influence import variance_inflation_factor col_count = model.exog.shape[1] vifs = [variance_inflation_factor(model.exog, i) for i in range(1, col_count)] pd.DataFrame(vifs, index=model.exog_names[1:], columns=["VIF"])
VIFの具体的な説明は省力しますが、値が大きければ大きいほど多重共線性を起こしている可能性が高いです。基準値は5, 10とされることが多いですが今回は10とすると、この値を超えているWalks(四球数)は回帰式から外した方が良いことがわかります。
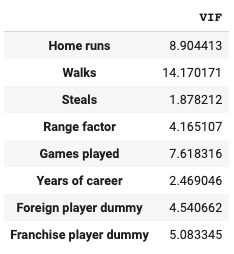
ちなみに、四球数が多重共線性を起こしている原因はHome runs(本塁打数)の影響を受けていることによる可能性があります。相手投手は本塁打数が多い強打者に対しては必然的に厳しい配球にせざる得ないため、四球が増えやすい、または敬遠などで四球数が増えている可能性があります。そこで本塁打数と四球数の相関係数を確認します。
df[['Home runs', 'Walks']].corr()

予想通り2つの変数間には強い正の相関があることがわかります。
回帰分析2
そこで四球数を除いて、回帰分析を再度回してみます。
df = df.drop(['Walks'], axis=1) Y = df[df.columns[1]] X = df[df.columns[2:]] X = sm.add_constant(X) model = sm.OLS(Y, X) results = model.fit() print(results.summary())
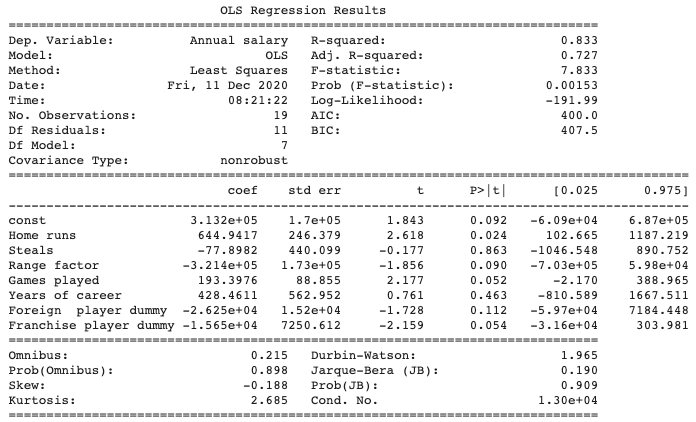
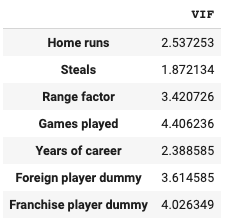
そして今回はVIFの値が全ての変数において十分低くなっていることがわかります。
考察
P値が有意水準を満たすのはHome runs(本塁打数)、Range factor(守備率)、Games played(出場試合数)、Franchise player dummy(生え抜き選手ダミー)の4つでした。coefを見ると本塁打を多く打ち、たくさん試合に出場すると年俸が上昇するということがわかります。逆に守備率が高いと年俸が下がるという結果が出ていますが、これは直感と反します。サブの選手は守備機会が少ないため、そもそも守備率が高く出やすい。一方で高い年俸を獲得している坂本、丸、岡本、小林選手などは守備の負担が大きいセンターラインやホットコーナーを守ることが多いので守備率が比較的低く出てしまう。その結果、このような分析結果が出ている可能性があります。そのため、守備率ではなく守備の正確性と守備機会が加算されていくような指標を使う必要があるかもしれません。また、生え抜き選手であると年俸が高くなるという当初の予測ははずれました。これは、陽選手や中島選手のようにFAなどで他球団から獲得した主力級の選手にはある程度高額な年俸が支払われている結果かもしれません。
いずれにせよ注意しなければいけないのは、今回の分析は信頼度が高いものではないという点です。理由はサンプル数が19と極端に少ないため、各説明変数の標準誤差が非常に大きくなってしまっているからです。また条件数も非常に高い値となっているため依然として多重共線性を起こしている可能性や統計的に問題がある可能性があるからです。より信頼できる結果を得るには12球団のデータを使ってサンプル数を大きくするなどの対応が必要です。
まとめ
今回はプロ野球選手の年俸を例に簡単な回帰分析をPythonで行いました。本記事を通してPythonを使った統計分析の流れをなんとなく理解していただけたら幸いです。明日は村山が若手エンジニアにおすすめの技術書を紹介してくれます。お楽しみに!